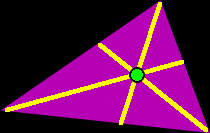
Centroid of a Triangle
The centroid of a triangle is kind of the center of the triangle -- if you try to balance the triangle on the tip of your finger, the centroid is where you'll put your finger to keep it level. The bisectors of each of the angles of the triangle intersect in the centroid. |
|
|
|

|
Chord
A chord on a circle is a line segment that connects two points that are on the outside edge (circumference) of the circle. |

|
|
|

|
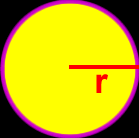
Circle
A circle is the set of points that all lie within a given distance of the center of the circle. This given distance is called the radius ( r in the pic on the right ).
For more info on circles, check out my Geometry of Circles page.
|

|
|
|

|
Circumference
The circumference is the perimeter (outer edge) of a circle. The formula for finding thecircumference of a circle is:
circumference = 
where 
|
|
|
|

|
Circumscribed
In the picture on the right, the circle is circumscribed about the triangle since each vertex of the triangle is touching the circle. |

|
|
|

|
Clockwise
Clockwise is when you are moving in the same direction as the arms on a clock. |
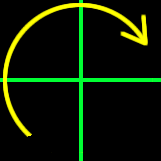
|
|
|

|
Coefficient
In a polynomial, the coefficients are the numbers that are right in front of the letters (the variables.)
Examples: In 5x-3y, the coefficients are 5 and -3.... x+7 is really 1x+7 and the coefficient is 1.
For more info on coefficients, check out my algebra lesson on Polynomials. |
|

|
Column
A column is a vertical stripe of something.
Usually, in math, it's a vertical stripe of numbers. (Remember that "vertical" means up and down.) |

|
|
|

|
Combinations
Combinations count how many different ways you can choose things from a set of objects.
Example: If you have three employees (A, B and C) and you want to form a committee of two, how many different ways can you do it? 3 ways...
A and B A and C B and C
For more info, check out my Combinations lesson. |
|

|
Combinatorics
Combinatorics is the study of counting.
For more info, check out my Combinatorics lessons. |
|

|
Commutative Property of Addition
The commutative property of addition is a math rule that is always true. Here it is with letters:
a + b = b + a
This rule just says that, when you are doing addition, it doesn't matter which order the numbers are in. You can add aand b OR you can add b and a ... and you'll get the same answer. Here it is with numbers so you can check this for yourself!
2 + 3 = 3 + 2
NOTE: This does not work with subtraction! |
|

|
Commutative Property of Multiplication
The commutative property of multiplication is a math rule that is always true. Here it is with letters:
a x b = b x a
This rule just says that, when you are doing multiplication, it doesn't matter which order the numbers are in. You can multiply a and b OR you can multiply b and a ... and you'll get the same answer. Here it is with numbers so you can check this for yourself!
2 x 3 = 3 x 2
NOTE: This does not work with division! |
|

|
Complementary Angles
Complementary angles are NOT angles that say "Oh, what a nice shirt and I just love the hair!" Those would be "complimentary angles" spelled with an "i".
In the picture on the right, angles A and B are complementary angles because their measures add up to 90 degrees:

|
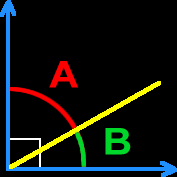
|
|
|

|
Complement of an Angle
Working from the idea of complementary angles in the definition above this,
the complement of an angle B is whatever size is necessary so that, if you stick them together, they make a 90 degree angle.
To find the complement of an angle, just subtract from 90...
Example: Find the complement of angle B whose measure is 30 degrees:
90 - 30 = 60... So, the complement is 60 degrees. Easy!
|
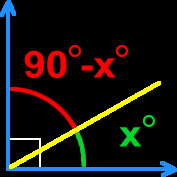
|
|
|

|
Complex Numbers
Before you hit algebra (and through most of algebra), you work with the Real Number System which is just all those regular numbers you're used to working with: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. This includes fractions, decimals and radicals made from these numbers. BUT, there is another number system out there! No, not THAT! Yes, it's all too true... It's the Complex Number System where a complex number is in the form:
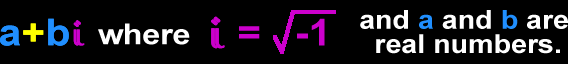
In higher math, you can do arithmetic, algebra and more with these goofy numbers. AND you can make very cool computer art with them -- Fractals. Check out my fractal gallery to learn more.
For more info on complex numbers, check out my algebra lessons on complex numbers. |
|

|
Composite
A number is composite if it has more than two factors. The number 20 is composite since it has more than two factors: 1, 2, 4, 5, 10, 20. The number 5 is NOT composite since it only has two factors: 1 and 5. The number 5 isprime. The number 1 is neither prime nor composite since it only has one factor: 1. |
|

|
Concave Polygon
Technically, if you can connect two vertices (the corners) of a polygon and have all or part of the line go OUTSIDE the polygon, then the polygon is concave. I just remember that, if there is a cave (like the kind a bear lives in), then it's concave. |

|
|
|

|
Cone
Ah, memories of childhood and ICE CREAM CONES! Wait, that was just last week. What was I talking about?
In geometry, a cone is formed by taking a circle (or an ellipse), and a line going up from the middle of the circle... Then a surface joins the top of the line and the edge of the circle. The cone in my picture on the right is a "right circular cone" since the line forming the height shoots up in a right angle (90 degrees) to the base (the circle.)
For info on conic sections, check out my conic sections lessons.
|
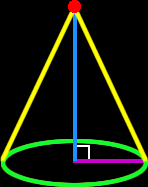
|
|
|

|
Congruent
Two objects are congruent if they are the same size and shape. In the pics on the right,

We use an equal sign with a little squiggle on top for the notation for congruent. |

|
|
|

|
Conjugate
You'll see conjugate pairs when working with radicals and complex numbers. I like to call them conjugate buddies, because they usually need to be with their friend in an algebra problem. Conjugate buddies are the same, but with the opposite sign. Here are two examples:

For more info on conjugates and how the complex kind are used in Algebra, check out my lesson on complex zeros.
|
|

|
Consecutive
Consecutive just means one right after the other.
Example: A list of consecutive whole numbers: 0, 1, 2, 3, 4, 5, 6, ...
Example: A list of consecutive even whole numbers: 0, 2, 4, 6, 8, ...
Example: A list of consecutive odd whole numbers: 1, 3, 5, 7, 9, ... |
|

|
Convex Polygon
You might want to scroll up and check out the definition of concave to really understand this one. It's easiest to just say that a convex polygon is one that is NOT concave! But, I'll let you think about this... A polygon is convex if you can draw straight lines that connect every single vertex and your lines never go outside the polygon. There is no cave! |

|
|
|

|
Coordinate
This is the same thing as Cartesian Coordinates...
Coordinates on the Cartesian plane are a set of numbers officially called "an ordered pair" that are in the form ( x , y ) ... The x guy is how far to the right or left you've counted over... and the y guy is how far up or down you've counted.
For more info on graphing with Cartesian coordinates, check out my Plotting Points lesson.
|
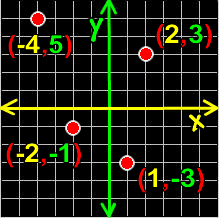
|
|
|

|
Coplanar
Any objects that lie in the same plane are called coplanar. |
|

|
Corresponding Sides and Angles
It's easier to show you this one than to tell you what it is in words. In similar triangles, like the ones in the picture on the right... One set of corresponding sides are A and D... One set of corresponding angles are a and d. Corresponding objects are in the same location. |
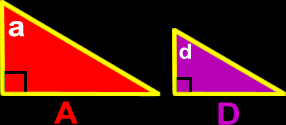
|
|
|

|
Counter-Clockwise
Counter-clockwise is when you are moving in the opposite direction as the arms on a clock. |
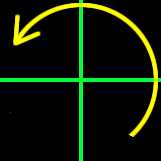
|
|
|

|
Cramer's Rule
Cramer's Rule is a method in algebra to solve systems of equations.
For more info on Cramer's Rule, check out my full lessons: Cramer's Rule for 2x2 Systems and Cramer's Rule for 3x3 Systems |
|

|
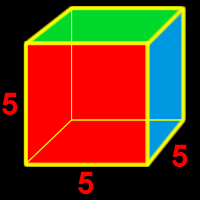
Cube
A cube is a box formed by putting six squares together, connected at the edges. Since all faces of a cube are squares, all the edges of the cube are the same length (which is 5in my picture on the right.)
The cube is one of the five Platonic Solids. For more info about Platonic solids, check out my Platonic solids gallery.
|
|
|
|

|
Cubic Equation
Used in Algebra, the critter below is cubic because of the x cubed and an equation because of the equal sign.
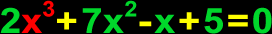
|
|

|
Cubic Polynomial
Used in Algebra, the critter below is a cubic polynomial because of the x cubed.
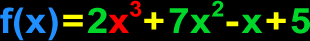
For more info on polynomials, check out my lesson, What's a Polynomial?
|
|

|
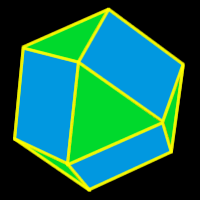
Cuboctahedron
The cuboctahedron is one of the semi-regular Platonic solids (a polyhedron.) It is created by either truncating (cutting off) the cube one half of the way into each edge or by truncating the octahedron one half of the way into each side.
Properties of the cuboctahedron:
14 faces: 8 equilateral triangles and 6 squares
12 vertices: 2 triangles, 2 squares
24 edges
Dihedral angle: about 125.27 degrees
For more info about Platonic solids, check out my Platonic solids gallery.
|
|
|
|

|
Cylinder
A cylinder is formed by taking two circles (or ellipses), putting one up above the other and wrapping a surface around to connect the edges. |

|
|