Polygons - Quadrilaterals

Properties of quadrilaterals, interior angles of quadrilaterals

Polygons:  Properties of Quadrilaterals

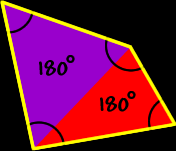
quadrilaterals

red line

Sum of the Interior Angles of Quadrilaterals:


quadrilaterals
 

To find the sum of the interior angles of a quadrilaterals, divide it up into triangles... There are two triangles...  Because the sum of the angles of each triangle is 180 degrees...  We get

quadrilaterals

So, the sum of the interior angles of a quadrilateral is 360 degrees.

red line

Regular Quadrilaterals - Squares:
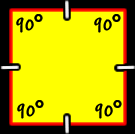
The properties of squares:

squares

All sides are the same length (congruent) and all interior angles are the same size (congruent).

To find the measure of the interior angles, we know that the sum of all the angles is 360 degrees (from above)...  And there are four angles...

squares

So, the measure of the interior angle of a square is 90 degrees.

red line

The measure of the central angles of a square:

squares

To find the measure of the central angle of a square, make a circle in the middle...  A circle is 360 degrees around...  Divide that by four angles...

squares

So, the measure of the central angle of a square is 90 degrees.