Algebra
In arithmetic, you always know what numbers you are working with... Like 8 - 2 = 6. In algebra, one or more of these numbers is unknown. They usually put an "x" in for the mystery number. Can you guess what x is here? 7 + x = 15. Easy! Of course, it gets a little harder than that... But, it's not bad.
I've got a ton of algebra lessons on the site! |
|

|
Algorithm
This is what they call it when Al Gore tries to dance. Ok, I know that was a really bad joke, but, typing out all these definitions is making me a bit loopy! An algorithm is a set of steps to complete a task. It may be the list of steps it takes to find the answer for a long division problem... Or it may be part of a computer program... It can even be the list of steps it takes for you to get ready to go to school in the morning. |
|

|
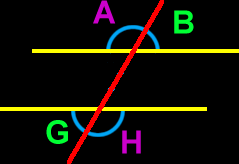
Alternate exterior angles
When a pair of parallel lines is intersected by a transversal (like in the diagram on the right), angles A and H are a set of alternate exterior angles and B and G are a set of alternate exterior angles.
In a drawing like this (where there is a set of parallel lines intersected by atransversal), alternate exterior angles are congruent (the same size.)
|
 |
|
 |
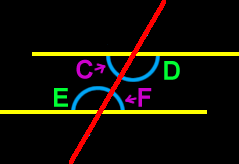
Alternate interior angles
When a pair of parallel lines is intersected by a transversal (like in the diagram on the right), angles C and F are a set of alternate interior angles and D and E are a set of alternate interior angles.
In a drawing like this (where there is a set of parallel lines intersected by atransversal), alternate interior angles are congruent (the same size.)
|
 |
|
 |
Alternating Sequence
An alternating sequence is a list of numbers that goes positive, negative, positive, negative... or negative, positive,negative, positive.
Example: -1, 2, -3, 4, -5, 6, -7, 8, ...
For more info on sequences, check out my "What's a sequence?" lesson. |
 |
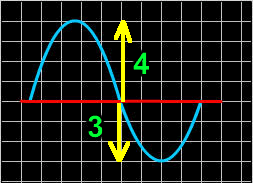
Amplitude
The amplitude of a graph or a curve is kind of the height of the graph... You take the height above the x-axis (4 in the pic on the right) and the height below the x-axis (3 in the pic) and add them together to get the amplitude (which is 4+3=7 in the pic). |
 |
|
|

|
Angle
An angle is the set of points (what is formed) when two rays both start at the same point. |
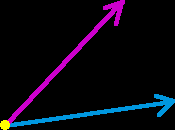 |
|
|

|
Annual
Annual means yearly or once a year. The term shows up in a lot of money problems in algebra. |
|

|
Annuity
Mathematically speaking, an annuity is a series of equal payments made over a specified period of time. For example, if you put a certain amount of money each month into a savings account, that would be an annuity. Mortgages, monthly health insurance payments, and pension payments are other types of annuities.
In the real world, an annuity is an investment (that you purchase) where you pay an annuity provider upfront to receive a certain amount of money each year or each month for a specified period. For example, when you retire, you can purchase a life annuity that pays out $1,000 each month for the rest of your life.

|
Arc
An arc of a circle is a segment of the circumference of the circle. |
 |
|
|

|
Area
Wow, you wouldn't believe how confusing the usual definitions for "area" in math dictionaries are! And it's such a simple thing. So, here's my explanation: If you are going to carpet a room, the amount of carpet you need IS the area. In the picture on the right, the area is the blue part.
For more info on areas, check out my reference page on area formulas. |
 |
|
|

|
Arithmetic
Working with numbers, arithmetic is the process and study of addition, subtraction, multiplication and division. |
|

|
Associative Property of Addition
The associative property of addition is a math rule that is always true. Here it is with letters:
a + ( b + c ) = ( a + b ) + c
Remember that you always do what's in the parenthesis ( ) first. This rule just says that, when you are doing addition, it doesn't matter which numbers you add first. You can add the a and b first OR you can add the b and c first and you'll get the same answer. Here it is with numbers so you can check this for yourself!
2 + ( 3 + 4 ) = ( 2 + 3 ) + 4
NOTE: This does not work with subtraction! |
|

|
Associative Property of Multiplication
The associative property of multiplication is a math rule that is always true. Here it is with letters:
a x ( b x c ) = ( a x b ) x c
Remember that you always do what's in the parenthesis ( ) first. This rule just says that, when you are doing multiplication, it doesn't matter which numbers you multiply first. You can multiply the a and b first OR you can multiply the b and c first and you'll get the same answer. Here it is with numbers so you can check this for yourself!
2 x ( 3 x 4 ) = ( 2 x 3 ) x 4
NOTE: This does not work with division! |
|

|
Average
This is the same thing as the "mean" of a group of numbers. It's weird to define "average" in words, but really easy to show what it is.
Look at this list of numbers: 3, 6, 13, 4, 9... Add them up and we get 35... Now, divide by how many numbers there are. There are five numbers, so divide 35 by 5... We get 7 and that's the average of this list of numbers. Notice that some of the numbers are above 7 and some are below. |
|

|
Axiom
An axiom is a rule in math that is always true. In fact, it is SO obviously
true that you don't have to prove it's true.
This is an axiom: The sun rises in the morning.
You know this is true and I don't have to prove it.
This is not an axiom: My cat is gold.
Yes, this is true, but how can you believe me without my proving it with a picture? Here's proof! >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> |
 |
|
|

|
Axis of Symmetry
An axis of symmetry is a line that cuts an object in half so that the two halves are mirror images of each other. The yellow lines on the right are both axes of symmetry. (The plural of "axis" is "axes.") |
 |
|