Polygons - Dodecagons

Properties of dodecagons, interior angles of dodecagons

Polygons:  Properties of Dodecagons

dodecagons

red line

Sum of the Interior Angles of a Dodecagon:

This image shows the process for a 
HEXAGON:
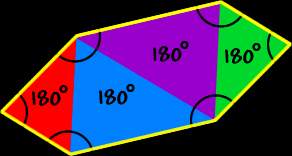
hexagons

Using the same methods as for hexagons to the right (I'll let you do the pictures)... 
To find the sum of the interior angles of a dodecagon, divide it up into triangles... There are ten triangles...  Because the sum of the angles of each triangle is 180 degrees...  We get

dodecagons

So, the sum of the interior angles of a dodecagon is 1800 degrees.

red line

Regular Dodecagons:
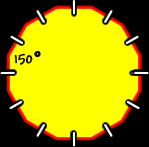
The properties of regular dodecagons:

dodecagons

All sides are the same length (congruent) and all interior angles are the same size (congruent).

To find the measure of the angles, we know that the sum of all the angles is 1800 degrees (from above)...  And there are twelve angles...

dodecagons

So, the measure of the interior angle of a regular dodecagon is 150 degrees.

red line

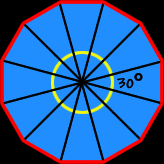
The measure of the central angles of a regular dodecagon:

dodecagon

To find the measure of the central angle of a regular dodecagon, make a circle in the middle (I'll let you do the picture)...  A circle is 360 degrees around...  Divide that by twelve angles...

dodecagons

So, the measure of the central angle of a regular dodecagon is 30 degrees.