Polygons - Nonagons

Properties of Nonagons, interior angles of Nonagons

Polygons:  Properties of Nonagons

nonagons

red line

Sum of the Interior Angles of a Nonagon:

This image shows the process for a 
HEXAGON:
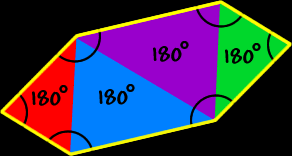
hexagons

Using the same methods as for hexagons to the right (I'll let you do the pictures)... 
To find the sum of the interior angles of a nonagon, divide it up into triangles... There are seven triangles...  Because the sum of the angles of each triangle is 180 degrees...  We get

nonagons

So, the sum of the interior angles of a nonagon is 1260 degrees.

red line

Regular Nonagons:
The properties of regular nonagons:

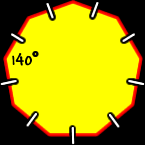
nonagons

All sides are the same length (congruent) and all interior angles are the same size (congruent).

To find the measure of the angles, we know that the sum of all the angles is 1260 degrees (from above)...  And there are nine angles...

nonagons

So, the measure of the angle of a regular nonagon is 140 degrees.

red line

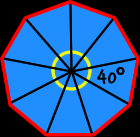
The measure of the central angles of a regular nonagon:

nonagon

To find the measure of the central angle of a regular nonagon, make a circle in the middle (I'll let you do the picture)...  A circle is 360 degrees around...  Divide that by nine angles...

nonagons

So, the measure of the central angle of a regular nonagon is 40 degrees.