12345678910
of 10

Rational Functions - The Whole Thing

Let's do another one:

Graph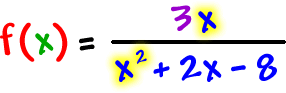f( x ) = ( 3x ) / ( x^2 + 2x - 8 )

2 things
and
2 sentences!

 

1The y-intercept:  Find f(0)
 

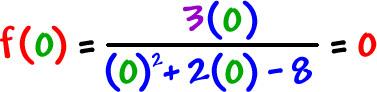
f( 0 ) = ( 3( 0 ) ) / ( ( 0 )^2 + 2( 0 ) - 8 ) = 0

( 0 , 0 ) nowhere else
 

2The x-intercept:  numerator = 0, solve.

 

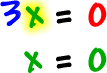3x = 0 ... x = 0

( 0 , 0 ) nowhere else

 
3Vertical asymptotes:  denominator = 0, solve
 
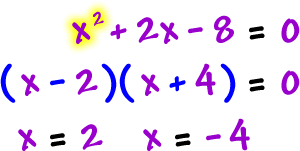x^2 + 2x - 8 = 0 ... ( x - 2 )( x + 4 ) = 0 ... x = 2 , x = -4The lines x = -4 and x = 2

 

4Horizontal asymptote:
 
Look at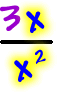3x / x^2

The line y = 0 ( the x-axis )

arrow
* When this is the case, we're going to be forced to "quickie plot" a few points to nail the graph.  No, this isn't being a sissy -- we'll have no choice.  But, Calculus will fix this problem by telling us where the graphs are increasing and decreasing!