123456
of 6

Freaky Factoring

That was easy...  So, we should be able to tackle this creep (who has the same pattern):

Factor

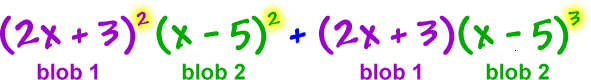
( 2x + 3 )^2 ( x - 5 )^2 + ( 2x + 3 )( x - 5 )^3 ... the ( 2x + 3 ) is blob 1 ... the ( x - 5 ) is blob 2
 

( 2x + 3 )^2 ( x - 5 )^2 + ( 2x + 3 )( x - 5 )^3 ... cross out the ^2 on the first blob, the ( x - 5 )^2, the ( 2x + 3 ) and the ^3 on the fourth blob = ( x - 5 )^2 ( 2x + 3 )[( 2x + 3 ) + ( x + 5 )] ... clean this up! ... = ( x - 5 )^2 ( 2x + 3 )( 3x - 2 )

 

Even though this looks like the messiest factoring you've ever done, it's really the easiest because the pattern will always work the same way in Calculus.

Factor this guy:

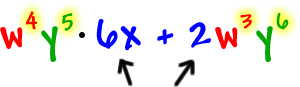
w^4 y^5 * 6x + 2w^3 y^6
Just deal with these separately.


This thing has the same shape:

Factor

( 2x - 3 )^4 ( 3x^2 - 1 )^5 ( 6x ) + 2( 2x - 3 )^3 ( 3x^2 - 1 )^6

( 2x - 3 )^4 ( 3x^2 - 1 )^5 ( 6x ) + 2( 2x - 3 )^3 ( 3x^2 - 1 )^6 ... cross out the ^4 on the first guy, ( 3x^2 - 1 )^5 , ( 2x - 3 )^3 and the ^6 on the last guy ... = 2( 2x - 3 )^3 ( 3x^2 - 1 )^5 [ 3x( 2x - 3 ) + ( 3x^2 - 1 )] = 2( 2x - 3 )^3 ( 3x^2 - 1 )^5 ( 9x^2 - 9x - 1 ) ... This last guy will never factor, so don't bother.