Do things improve?  Yep!  (Whew.)

Look at the tangent lines on the right...
 

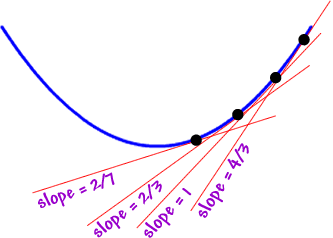
Not only are those slopes positive, they are getting bigger.  This is when you start celebrating!

In Calculus, you'll be doing a lot of hunting for those horizontal tangent lines because that's where interesting stuff happens: maximums, minimums, changing from increasing to decreasing and changing from decreasing to increasing.

While we're here, I want to point out a couple more things to you.

Look at the mountain again.
 

Notice that it's shaped like an upside down bowl...  In Calculus, you'll call this "concave down."  Let's take another look at those slopes:
 

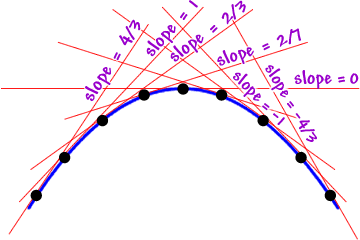
Here's the list in order from left to right:

Notice that the slopes of the tangent lines are decreasing.