We'd start Cramer's Rule by finding D:
![D = [ row 1: 1 , 3 row 2: 2 , 6 ] = 0](/sites/default/files/images/07-matrices-35.gif)
and we'd get stuck with
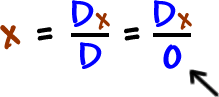 |
and |
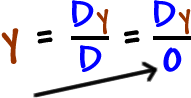 |
BIG TROUBLE!
So, this all ties together!
If the determinant of the coefficient matrix is zero, then the system does not have a nice ( x , y ) solution. (Remember that the lines could be parallel, or they could be the same line.) AND, if the determinant of a matrix is zero, then the matrix does not have an inverse... So, we can't get a nice ( x , y ) solution!
YOUR TURN:
(and be sure to do a quick check on the determinant before you start in on the inverse):
Use inverse matrices to solve:
![]()
![]()
Use inverse matrices to solve:
![]()
![]()