12
of 2

Maximums and Minimums

Now, for the relative minimums...  Those are the bottoms of the valleys:

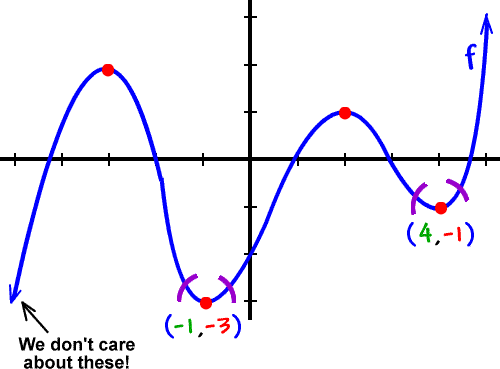
the relative minimums of the graph are -3 at x = -1 and -1 at x = 4 ... we don't care about the points in the interval ( -infinity , -3 )

Relative mins are the lowest points in their little neighborhoods.

f has a relative min of -3 at x = -1.

f has a relative min of -1 at x = 4.

YOUR TURN:

Find the relative extrema:

find the relative extrema

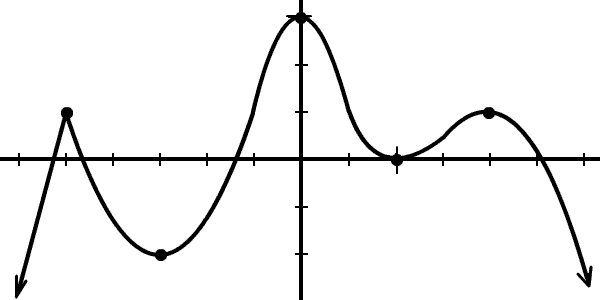
So, how many relative mins and maxes does the typical polynomial critter have?

Don't know?  When in doubt, draw pictures!

Let's draw some possible shapes of

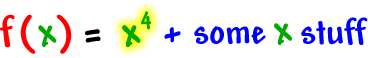
f ( x ) = x^4 + some x stuff

Remember, we use how many real zeros he might have to guide us.

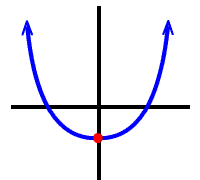
an x^4 guy with four real zeros and three relative extrema an x^4 guy with two real zeros and three relative extrema a plain x^4 guy with two real zeros and one relative minimum

a plain  x^4

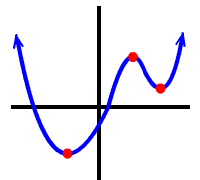
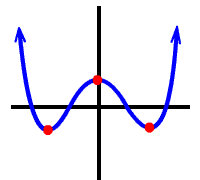
Hmm...  It looks like an  x^4 guy can have, at most, 3 relative extrema.

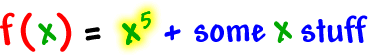What about   f ( x ) = x^5 + some x stuff ?

(I'll let you do the drawing.)

 

It looks like an x^5 guy can have, at most, 4 relative extrema.

I smell a theorem brewing!  (Either that or it's because I didn't shower this morning.)

A polynomial of degree n can have, at most, n - 1 relative extrema.