1234
of 4

Complex Zeros

There's one more biggie.

Remember that theorem about real zeros?

An nth degree polynomial has, at most, n real zeros.

Well, dude, now that we have complex zeros, we can say this:

An nth degree polynomial has
EXACTLY  n  ZEROS!*

*This includes real and complex.

So, now, if we have a 3rd degree polynomial...  we WILL get 3 zeros!

Check it out:

Find the zeros of:

f ( x ) = x^3 + 16x

then draw a rough sketch of the graph:

What's his basic shape?

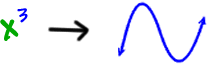
x^3 ... basic cubic shape

Let's find those zeros:

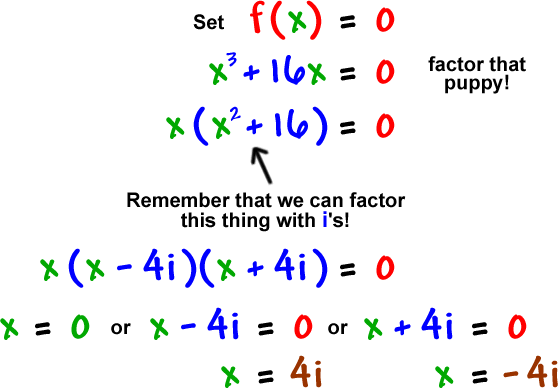
Set f ( x ) = 0 ... x^3 + 16x = 0 ... factor that puppy! ... x ( x^2 + 16 ) = 0 ... remember that we can factor this thing with i's! ... x ( x - 4i ) ( x + 4i ) = 0 gives x = 0 or x- 4i = 0 or x + 4i = 0 which gives x = 4i and x = -4i

 

zeros:

0 ( real ) ... this is a shoot through ... -4i , 4i ( complex buddies ) ... these won't show up on the graph

The best we can do here is to make our best guess at the graph based on what we have...

possible graph ... 3rd degree polynomial with a zero at x = 0

or

possible graph ... 3rd degree polynomial with a zero at x = 0

Check it on the graphing calculator!  (You probably won't see any wobble at all.)