1234
of 4

Real Zeros

Let's try a messier one:

Find the real zeros of

f ( x ) = ( x + 5 ) ( x + 2 ) ( x - 3 ) ( x - 7 )

then draw a rough sketch of the graph. 

Well, it sure looks creepy...  but, it isn't!  First of all, if we multiplied this mess out, the leading term would be

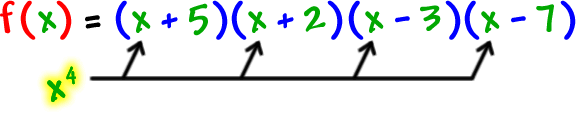
f ( x ) = ( x + 5 ) ( x + 2 ) ( x - 3 ) ( x - 7 ) ... the first terms multiply together to give x^4
So, his basis shape is  

Let's find the zeros...

Set  f ( x ) = 0and solve...

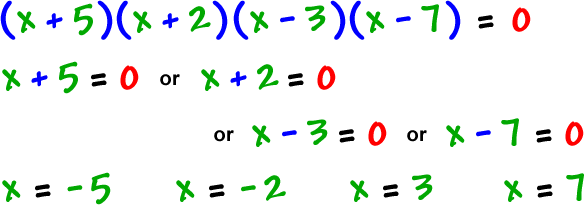
( x + 5 ) ( x + 2 ) ( x - 3 ) ( x - 7 ) = 0 gives x + 5 = 0 or x + 2 = 0 or x - 3 = 0 or x - 7 = 0 which gives x = -5 , x = -2 , x = 3 , and x = 7

real zeros: -5, -2, 3, 7

Draw it!

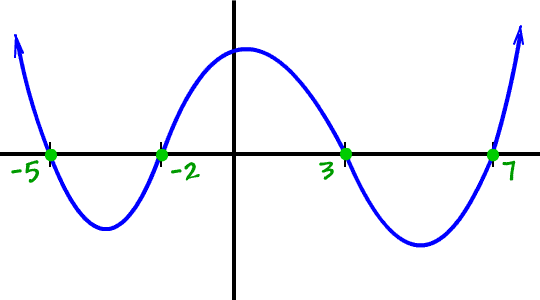
graph of f ( x ) = ( x + 5 ) ( x + 2 ) ( x - 3 ) ( x - 7 ) = 0 ... the zeros are -5, 2, 3, and 7

*Remember, this is just a rough sketch!

Hey!  Why don't you check this on the graphing calculator?

If you'd multiply him all out, he'd be

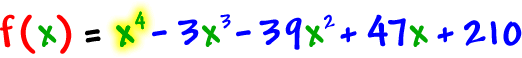
f ( x ) = x^4 - 3x^3 - 39x^2 + 47x + 210

So, you'll enter him as

x^4-3x^3-39x^2+47x+210

But, there's one more thing we need to do...

It turns out that this guy is REALLY tall!

Go ahead and hit theEVALbutton to graph him and you'll see
what I mean.  

To get the full picture, let's change the settings at the bottom of the calculator...  See them?  Set them to:

Xmin: -6.0 , Xmax: 8.0 , Ymin: -300 , Ymax: 250

Cool, huh?