As we saw in the previous lessons, when a parabola is in the form

it's pretty easy to graph.

The only problem is...  They usually aren't in this form!  (D'oh.)

You might need to graph something like this:

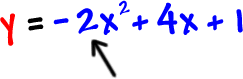
Well, we can see by the   that this IS a parabola... 
and that it will be upside down

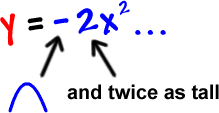
But, other than that, it's impossible to tell.

The "+ 4x + 1" part means that there's some sort of shifting going on, but we can't see what it is.

We'll need some way to get this thing in our easy graphing form:

The amazing trickery that will get our desired result is called completing the square.  It's not too bad, once you get used to it.