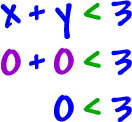Ok, now you're an expert at
graphing lines like
But, what if we stick an inequality in there?
Don't worry. If you use your head, it's not that bad. It's just one more thing to worry about.
Let's graph the line:
 |
|
||||||||
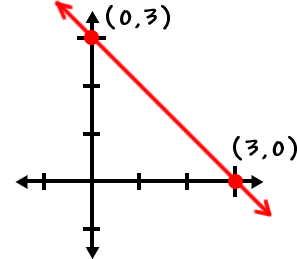?Remember that this rectangular coordinate grid is just made up of a bunch of ( x , y ) points.
All the points ON the line work in this part:
Now, we just need to find all the points that work in this part:
Here's how we find these points:
We just pick a point OFF the line and test it!
 |
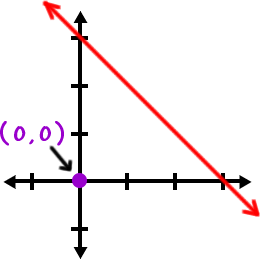The origin,
( 0 , 0 ), is really
easy to work with, so let's
try it:
|
Here's the deal:
If
( 0 , 0 )
works, then ALL the points
on the same side of the line will
work.
Don't believe me? Let's try a couple more:
 |
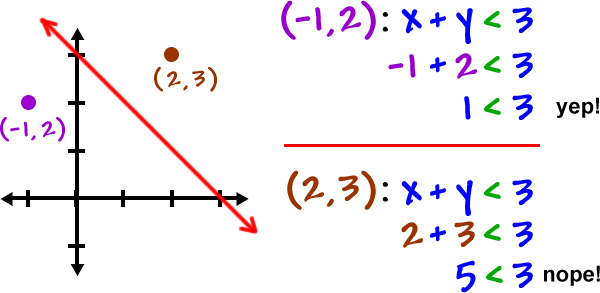So, our answer is this:
 |
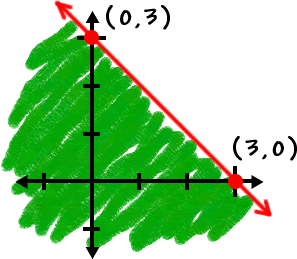All the
( x , y )
points on the line and in the
shaded region work in
|
