SOME NUMERICAL EXAMPLES:
EXAMPLE 1:
Let's look at the sequence whose nth term is given by n/(n+1). Recall, that we letn=1 to get the first term of the sequence, we let n=2 to get the second term of the sequence and so on.
What will this sequence look like?
1/2, 2/3, 3/4, 4/5, 5/6,... 10/11,... 99/100,... 99999/100000,...
What's happening to the terms of this sequence? Can you think of a number that these terms are getting closer and closer to? Yep! The terms are getting closer to 1! But, will they ever get to 1? Nope! So, we can say that these terms are approaching 1. Sounds like a limit! The limit is 1.
As n gets bigger and bigger, n/(n+1) gets closer and closer to 1...
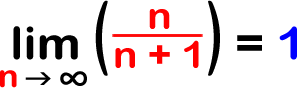
EXAMPLE 2:
Now, let's look at the sequence whose nth term is given by 1/n. What will this sequence look like?
1/1, 1/2, 1/3, 1/4, 1/5,... 1/10,... 1/1000,... 1/1000000000,...
As n gets bigger, what are these terms approaching? That's right! They are approaching 0. How can we write this in Calculus language?
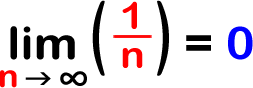
What if we stick an x in for the n? Maybe it will look familiar... Do you remember what the graph of f(x)=1/x looks like? Keep reading to see our second example shown in graphical terms!