1234567
of 7

Gauss's Problem and Arithmetic Series

Do you think we can find a formula that will work for adding all the integers from 1 to n?

1 + 2 + 3 + ... + n

Think about it!  Look over the last three problems we just did -- see anything?

Let's write it out the same way:

1 + 2 + 3 + ... ... + ( n - 2 ) + ( n - 1 ) + n ... 1 and n add up to ( n - 1 ) ... 2 and ( n - 1 ) add up to ( n- 1 ) ... 3 and ( n - 2 ) add up to ( n - 1 )

How many pairs of n + 1 are there?  Half of n!

n / 2 pairs of n + 1

 

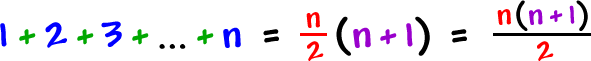1 + 2 + 3 + ... + n = ( n / 2 )( n + 1 ) = ( n( n + 1 ) ) / 2

 

TEST IT:

Find the sum

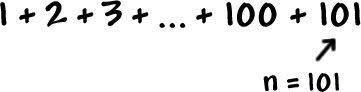
1 + 2 + 3 + ... + 100 + 101 ... n = 101

(You know it will be 5050 + 101 = 5151.)

Does the formula work?

How would you write this series in sigma notation?

1 + 2 + 3 + ... + 101