Online Math Dictionary: P

Easy to understand math definitions for K-Algebra mathematics
Just scroll down or click on the word you want and I'll scroll down for you!

parabola	parallel	parallelogram
Pascal's triangle	pentagon	pentagram
percent	perimeter	permutations
perpendicular	pi	piecewise function
point	polygon	polyhedron
polynomial	positive numbers	prime
prism	probability	product
proof	proper fraction	proportion
pyramid	Pythagorean Identities	Pythagorean Theorem
Pythagorean triples

Parabola
The formula for the standard parabola is

For more info and examples, check out myParabola lesson.
For graphing parabolas, check out my Graphing Parabolas lessons (first in a series).

parabola

Parallel
Two lines (lying in the same plane) are parallel if they never intersect... This means that the two lines are always the same distance apart.

parallel lines

Parallelogram
A parallelogram is a quadrilateral (a four sidedpolygon) where both pairs of opposite sides are parallel.
For more info, check out Properties of Parallelograms.

parallelogram

Pascal's Triangle Pascal's triangle was created by a French mathematician named Blaise Pascal. To build the triangle, start with the three 1's at the top and put 1's down the sides. To get the numbers in the middle, you add the two numbers right above. To get the 4, you add 1+3. To get the 10, you add 4+6.
So, what's the next line? 1 6 15 20 15 6 1 And it just keeps going! For more advanced info, check out my Binomial Theorem lesson and my Binomial Theorem Revisited lesson.

Pentagon
A pentagon is a five sided polygon. The pentagon in the picture on the right is a regular pentagon because all the sides and angles are the same (congruent).

For more info on hexagons, check out my properties of pentagons page.

pentagon

Pentagram
A pentagram is made by connecting the vertices of a pentagon with straight lines. Then, thepentagon is erased. You can also make hexagrams from hexagons, octagrams fromoctagons and so on.

For a related brain bender, check out The Handshake Puzzle.

pentagram

Percent
Percents are like fractions and decimals because they count PART of something. Whole numbers (0, 1, 2, 3, ...) count whole things -- like a whole pizza. You can use a percentages to count part of the pizza. Half of a pizza would be 50% of a pizza. One-fourth of a pizza would be 25% of a pizza.

Examples: 20% 0.05% 245.2%

Perimeter
Pretend that the shape on the right is a big park... The perimeter is the amount offencing you'd need to close it all in.

For more info on perimeters, check out my reference page on perimeter formulas.

perimeter

Permutations
A permutation is an arrangement of objects.
Example: How many ways can you arrange the letters A, B and C? 6 ways
ABC ACB BAC BCA CAB CBA
For more info, check out my Permutations lesson.

Perpendicular
Two lines are perpendicular if they intersect in a 90 degree (right) angle.

perpendicular

Pi
In a circle, pi is the ratio of the circumference to the diameter.
pi = circumference/diameter

pi = circumference/diameter

Pi is an irrational number (which means that its decimal part goes on forever and never repeats.)

circle

Piecewise Function
A piecewise function is a function that is defined (and graphed) in two or more pieces.
For more info, check out my lesson on Graphing Piecewise Functions.

piecewise defined function

Point
A point is a location in space. I can't even draw you a real picture of a point, because my dot would really be a blob of points. It's impossible to really draw just one point. So, when you're in Algebra and you have to graph points, you'll just have to pretend.

Polygon
A polygon is a geometric shape made up of vertices that are connected with line segments.

For more specific info, check out one of my "Properties of" pages on triangles,quadrilaterals, pentagons, hexagons, heptagons, octagons, nonagons, decagons, 11-gonsor dodecagons.

polygon

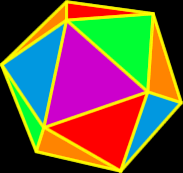
Polyhedron
A polyhedron is a three-dimensional object whose faces are polygons. The most famous set of polyhedra (that's the plural) is the five Platonic Solids that may have been discovered by Pythagoras. These solids are special because they are the only ones that are made up of regular polygons. They are the tetrahedron, the cube (hexahedron), the octahedron, the dodecahedron and the icosahedron.
For more info, check out my Polyhedra Gallery.

polyhedron - icosahedron

Polynomial
For now (and probably forever), you can just think of a polynomial as a bunch of blobs that are being added and subtracted. The blobs are just products of numbers and variables (letters) with exponents. Here's an example:

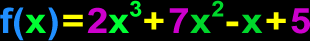
For more info and more examples, check out my Polynomial lessons.

Positive Numbers
Positive numbers are those that appear to the right of zero on the number line.

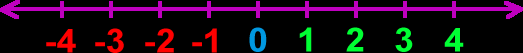Prime
A number is prime if it has exactly two factors: 1 and itself. The number 20 is not a prime number since it has more than two factors: 1, 2, 4, 5, 10, 20. The number 20 is composite. The number 1 is neither prime nor composite since it only has one factor: 1.
Here are some prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ...

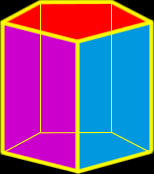
Prism
A prism is a polyhedron that is formed with two parallel polygons (the bases - top and bottom)that are connected at the edges with rectangles. My example in the picture is a right prism since the sides form right (90 degree) angles with the bases.

prism

Probability
A probability tells us how likely it is for an event to occur. When the weatherman says there's a 60% chance of rain, that's a probability. When you toss a coin, there's a 50% (1/2) probability that "tails" will come up.
Let's look at rolling a die... There are 6 possible rolls (1, 2, 3, 4, 5, 6). This number goes in the denominator. What if we want to know the probability for rolling a 5... There is one 5 on a die... So, there's one chance out of six that we'll roll a 5. That's a 1/6 probability. What if we want to roll an odd number? There are three odd numbers on a die (1, 3, 5)... That's three chances out of six... That's a 3/6 (or 1/2) probability.

Product
The product is the answer when you multiply two (or more) numbers.
Example: 3 x 2 = 6
For more info, check out my Multiplication Lessons.

Proof
A proof is an argument that shows something (like a theorem) is true beyond any doubt. In math, sometimes a proof is all numbers and symbols and sometimes there are sentences too.
There are different kinds of formal proofs in math: direct proof, indirect proof and mathematical induction, to name a few.

Proper Fraction
Proper fractions really aren't any more correct than improper fractions, but elementary school teachers like you to use them. A proper fraction is when the numerator is less than the denominator.
For more info on fractions, check out my lessons on fractions.

$proper fraction$

Proportion
A proportion is simply two ratios that are equivalent to each other. Proportions are usually used in Algebra to solve for some missing information.

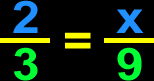
proportion: 2/3 = x/9

Protractor
A protractor is a device used in Geometry to measure and draw angles.

Pyramid
A pyramid is formed when triangles are put on a polygon base (a square in my picture). These triangles meet at a single vertex above the base.

pyramid

Pythagorean Identities
The Pythagorean Identities are

For more info on the Pythagorean Identities and where they come from, check out my Pythagorean Identities lesson.

Pythagorean Theorem
This is kind of creepy in words, but an easy equation. Here are the words: The sum of the squares of the lengths of the legs of a right triangle is equal to the square of the length of the hypotenuse.

Pythagorean Theorem: a^2+b^2=c^2

Pythagorean Theorem

Pythagorean Triples
Pythagorean triples are also called Pythagorean numbers. These are whole numbers that work together in the Pythagorean theorem.

A

B

C

D

E

F

G

H

I

no
J's

K

L

M

N

O

P

Q

R

S

T

U

V

W

no
X's

no
Y's

no
Z's