|
on the unit circle. |
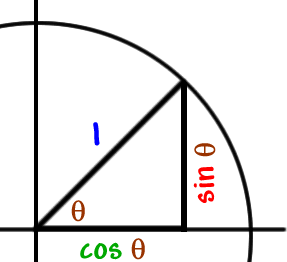 |
|
|
|
|
|
|
But, can you remember the other two? If you forget, here's the quick way to get them from the first one:
![[ sin^2( theta ) / sin^2( theta ) ] + [ cos^2( theta ) / sin^2( theta ) ] = 1 / sin^( theta )](/sites/default/files/images/29-trigonometry-07.gif)
|
|
(You can also remember that the "co"
guys go together!)
![[ sin^2( theta ) / cos^2( theta ) ] + [ cos^2( theta ) / cos^2( theta ) ] = 1 / cos^2( theta )](/sites/default/files/images/29-trigonometry-09.gif)
|
|
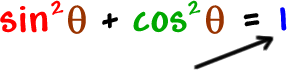
Let this one guide you...
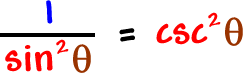 |
|
||||||||
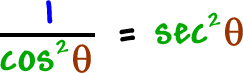 |
|
||||||||
You'll still be doing a lot of simplifying of trig expressions in Calculus, and these come up a lot!