Remember this notation?
![]()
This is a lesson on composition of functions... But, not like you think!
In Calculus, you're going to need to look at this in a different way...
Look at this guy:
![]()
When I look at this, I see two things:
AN OUTSIDE: | AN INSIDE: | |
|
| |
| call it | call it | |
|
| So, |
The cool thing is that, for this, we don't need all that messy notation. We just need to be able to find the levels!
Levels often (but, not always) announce themselves with parentheses or the word "of" as you read it.
Like | 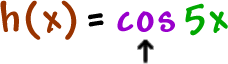 | |
| Read it! "Cosine OF 5x." | ||
| outside | |
inside |