123456
of 6

Rational Functions - More on Limits

Remember end-tail behavior?  What's going on with those tails?

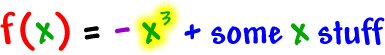
f( x ) = -x^3 + some x stuff
 

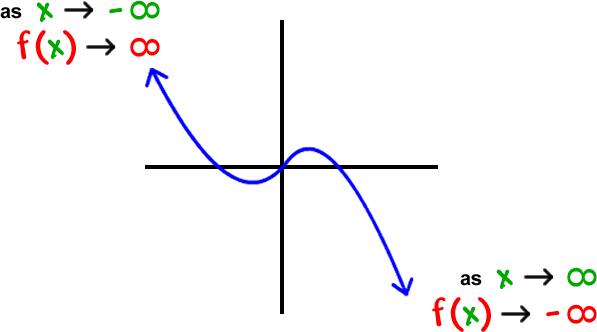
graph of f( x ) = -x^3 + some x stuff ... as x goes toward -infinity , f( x ) goes toward infinity ... as x goes toward infinity , f( x ) goes toward -infinity
 

This was called "finding limits."

One of the things math geeks get all jazzed about in Calculus is seeing what happens when x goes toward infinity and x goes toward -infinity.

We can do this with these rational function critters, too.  The key here is that horizontal (or slant) asymptote.

Check it out:

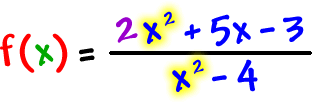
f( x ) = ( 2x^2 + 5x - 3 ) / ( x^2 - 4 )


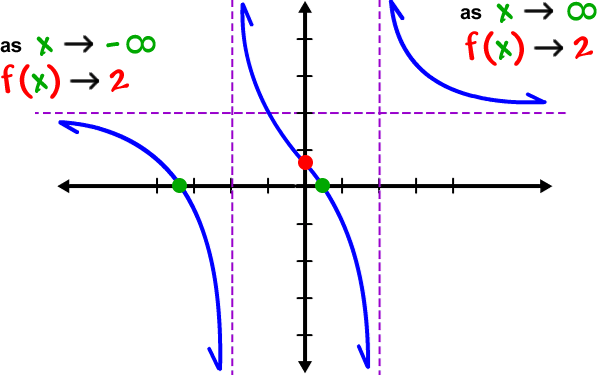
graph of f( x ) = ( 2x^2 + 5x - 3 ) / ( x^2 - 4 ) ... as x goes toward -infinity , f( x ) goes toward 2 ... as x goes toward infinity , f( x ) goes toward 2
 

Remember...  GRAPHS HUG ASYMPTOTES!

As x gets bigger and bigger (goes to the right), our graph gets closer and closer to that asymptote (which is y = 2.)  It will never actually hit the asymptote ( f(x) will never = 2), it will just get closer and closer.  This is why we use the word "approaches."  It's the same story on the left when x is getting smaller and smaller.