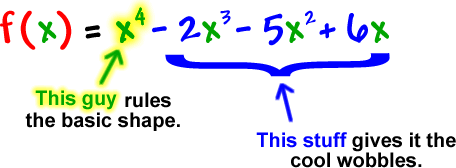
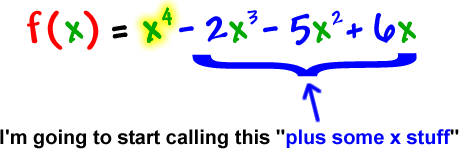12345
of 5

Basic Shapes - Even Degree (Intro to Zeros)

Check out this guy:

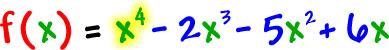
f ( x ) = x^4 - 2x^3 - 5x^2 + 6x

Stick him into the graphing calculator and see what happens!

x^4-2x^3-5x^2+6x

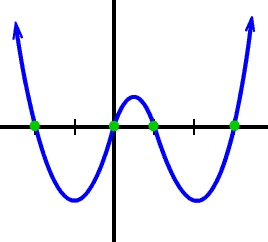
Your graph should look like this:

Graph of f ( x ) = x^4 - 2x^3 - 5x^2 + 6x

Two things to notice here:
 
1Both tails shoot up
2This guy crosses the x-axis
4 times... 
What's his degree?  4!

Repeat after me... Duuuuuude!

(We aren't going to worry at all about how high the mountains are and how low the valleys are.  We'd really need Calculus to nail this info.)

f ( x ) = x^4 - 2x^3 - 5x^2+ 6x ... I'm going to start calling everything but the x^4 "plus some x stuff"

f ( x ) = x^4 - 2x^3 - 5x^2 + 6x ... the x^4 rules the basic shape, the other stuff gives it the cool wobbles