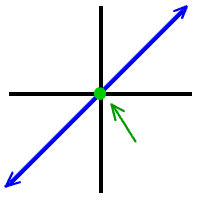
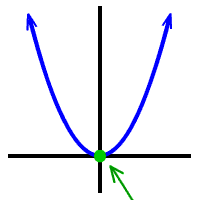
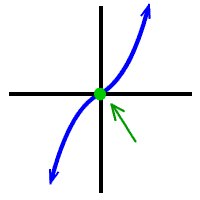
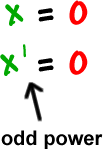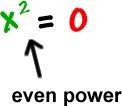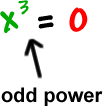1234
of 4

Multiplicities

OK, check out these graphs...

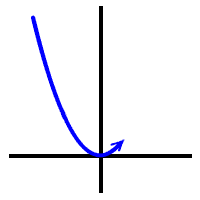
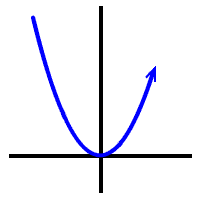
Look at HOW they hit the x-axis...

f ( x ) = x

f ( x ) = x^2

f ( x ) = x^3

graph of f ( x ) = x

graph of f ( x ) = x^2

graph of f ( x ) = x^3

The first one and the last one are what I call "shoot throughs."  They shoot through the x-axis.

The middle guy "kisses" the x-axis:

the graph of f ( x ) = x^2 comes in towards the x-axis

the graph of f ( x ) = x^2 kisses the x-axis

the graph of f ( x ) = x^2 goes away from the x-axis

It comes in...

kisses...

then goes away.

Notice what happens when we get the zeros...

f ( x ) = x
x = 0 is x^1 = 0 ... odd power

 

f ( x ) = x^2
x^2 = 0 ... even power

f ( x ) = x^3
x^3 = 0 ... odd power

*When the power on a zero is odd, it's a shoot through.

*When the power on a zero is even, it's a kiss.