12
of 2

Maximums and Minimums

Check out this graph:

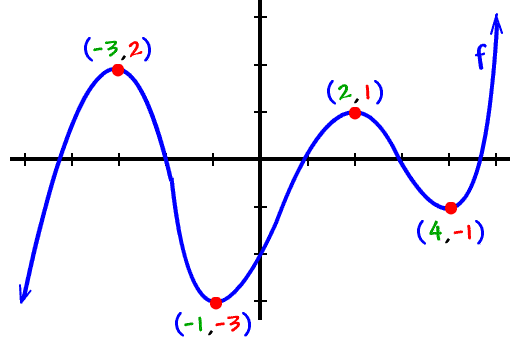
a graph of a polynomial with relative extrema at points ( -3 , 2 ) , ( -1 , -3 ) , ( 2 , 1 ) and ( 4 , -1 )

The tops of the mountains are relative maximums because they are the highest points in their little neighborhoods (relative to the points right around them):

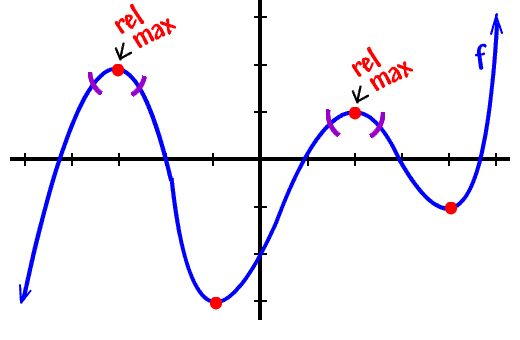
the relative maximums are the highest points on the "mountains" of the graph

Suppose you're in a roomful of people (like your classroom).  Find the tallest person there.  (It's usually a guy.)  He is the relative max of that room.  Specifically, he's the tallest relative to the people around him.   But, what if you took that guy to an NBA convention?  There'd be lots of guys who beat him.

Look back at the graph...

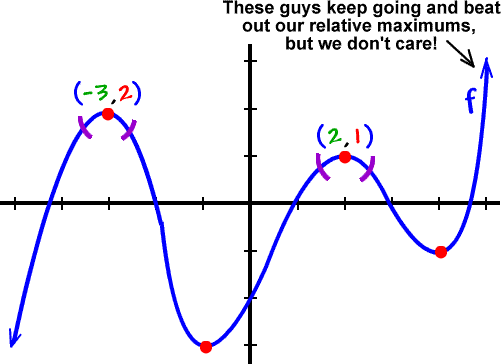
the relative maximums of the graph are 2 at x = -3 and 1 at x = 2 ... the guys in the interval ( 4 , infinity ) keep going and beat out our relative maximums, but we don't care!

(Relative extrema (maxes and mins) are sometimes called local extrema.)

Other than just pointing these things out on the graph, we have a very specific way to write them out.

Officially, for this graph, we'd say:

f has a relative max of 2 at x = -3.

f has a relative max of 1 at x = 2.

The max is, actually, the height...  the x guy is where the max occurs.

So, saying that the max is (-3, 2) would be unclear and not really correct.