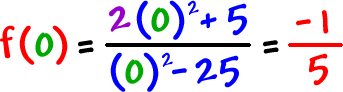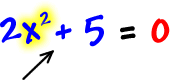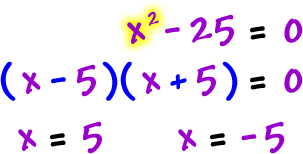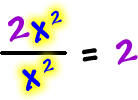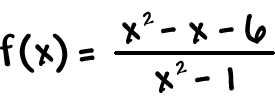123
of 3

Putting It All Together

OK...  what were the 2 things?
 

1

intercepts

2

asymptotes

What were the 2 sentences?

1

These guys are functions.

2

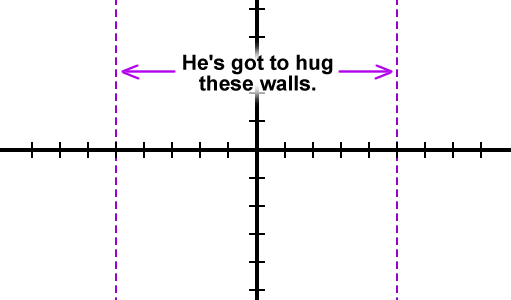
Graphs hug asymptotes.

Let's do some graphing, baby!

Graph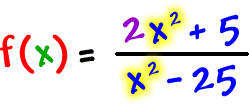
 		f ( x ) = ( 2x^2 + 5 ) / ( x^2 - 25 )
 

2 things
and
2 sentences!
 


1
 


The y-intercept: Find f(0)
 

f ( 0 ) = ( 2 ( 0 )^2 + 5 ) / ( ( 0 )^2 - 25 ) = -1/5

( 0 , -1/5 ) ... nowhere else!


2
 


The x-intercept: Set numerator = 0 and solve
 

2x^2 + 5 = 0
Since we only deal with real numbers when graphing, this has no solution!
*Do you see why?


It will never cross the x-axis.
This is going to be very useful info!


3
 


Vertical asymptotes: Set denominator = 0 and solve
 

x^2 - 25 = 0 gives ( x - 5 ) ( x + 5 ) = 0 which gives x = 5 and x = -5

The lines x = -5 and x = 5

 

4
 

Horizontal asymptote:
 

Look at

 

( 2x^2 ) / ( x^2 ) = 2

 

The line y = 2

 

Now we're ready to graph...  Remember that plotting points is for sissies, so use your brain!

First, let's get our intercepts and asymptotes on the graph:

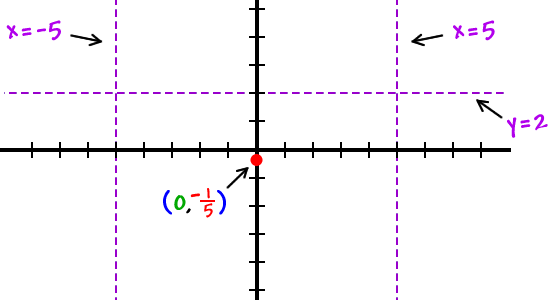
intercept: ( 0 , -1/5 ) , no x intercept ... and asymptotes x = -5 , x = 5 , and y = 2

*Remember the the graph CANNOT cross the y-axis anywhere else and it CANNOT cross the x-axis at all!

Now, we use our brains and our sentences...

These are the three neighborhoods that this graph lives in:

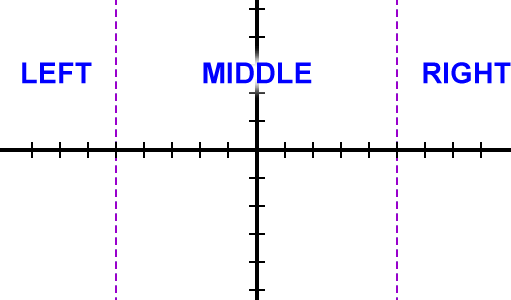
The three neighborhoods in our grpah: left, middle, and right

Let's look at the left neighborhood:
*Remember your 2 sentences!

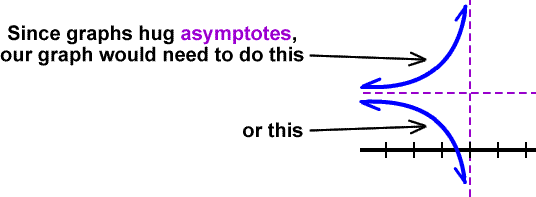
possible graphs for the left section ... since graphs hug asymptotes, our graph would need to do this or this

Since he's a function (and must pass the vertical line test), he can't do both.

What did we say about crossing the x-axis for this guy?  (Look back if you need to.)

Yep -- he's not allowed to cross the x-axis!  But, look at that bottom guy:

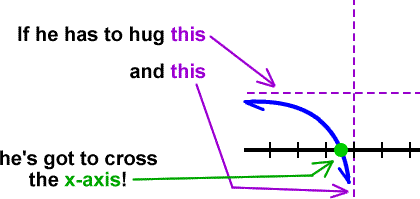
a possible graph for the left section ... If he has to hug the y = 2 asymptote and the x = -5 asymptote, he's got to cross the x-axis!

But, he's not allowed to -- so, he's got to live upstairs!

We can use the same reasoning for the right neighborhood:

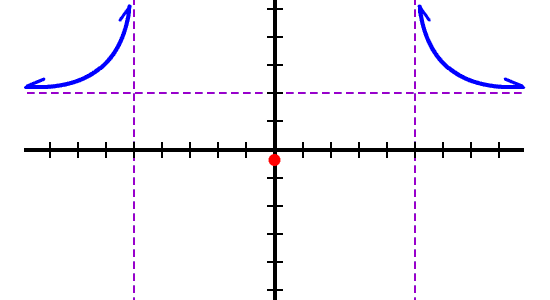
the left and right sections of the graph of f ( x ) = ( 2x^2 + 5 ) / ( x^2 - 25 )

What about the middle neighborhood?

He's got to hug these walls. (the asymptotes x = -5 and x = 5)

And remember, he's not allowed to cross the x-axis!  So, he CAN'T do any of these things:

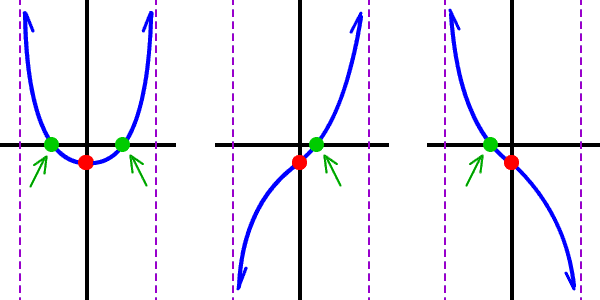
possibilities for the middle section of the graph

What's left?

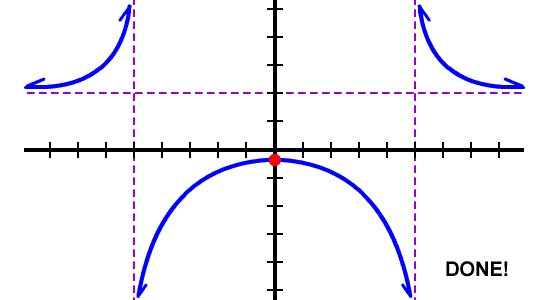
graph of f ( x ) = ( 2x^2+ 5 ) / ( x^2 - 25 ) ... DONE!

 

YOUR TURN:

Graph

f ( x ) = ( x^2 - x - 6) / ( x^2 - 1 )

  (You already have all the pieces!)

Hey, you can check it on the graphing calculator!  Enter it in like this:

( x^2 - x - 6 ) / ( x^2 - 1 )