12
of 2

Increasing and Decreasing Revisited

Let's look back at some of the critters we graphed in the last section and find the intervals where they are increasing and decreasing.

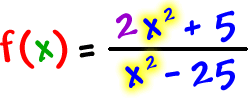
f ( x ) = ( 2x^2 + 5 ) / ( x^2 - 25 )

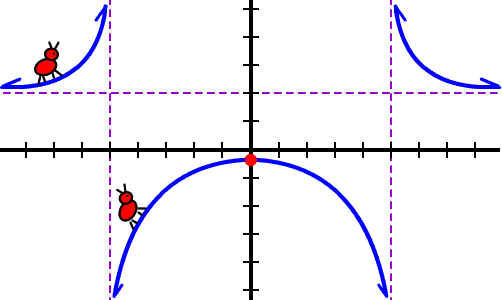
graph of f ( x ) = ( 2x^2 + 5 ) / ( x^2 - 25 ) ... Pierre is climbing uphill on ( -infinity , -5 ) and ( -5 , 0 )

Increasing?  Pierre the Mountain Climbing Ant is walking uphill...  Remember that Pierre always walks from left to right for these.

f is increasing on

  ( -infinity, -5 ) U ( -5 , 0 )

*Remember to answer with interval notation using x values.

Why did we leave the -5 out?  Because the graph doesn't even exist there!

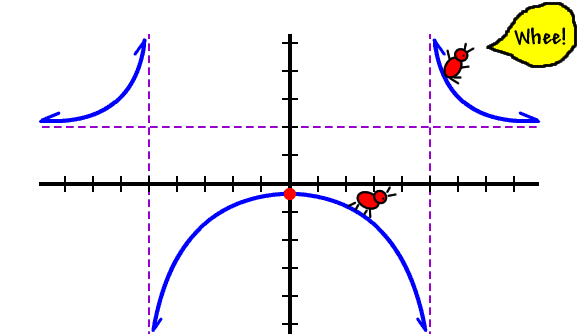
Decreasing?  Pierre is walking downhill...

graph of f ( x ) = ( 2x^2 + 5 ) / ( x^2 - 25 ) ... Pierre is sliding downhill (Whee!) on ( 0 , 5 ) and ( 5 , infinity )

f is decreasing on

  ( 0 , 5 ) U ( 5, infinity )