Here's the first one:
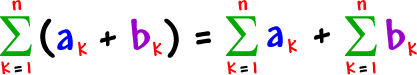 |
Here's an example so you can believe it:
Find this sum:
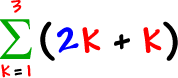
Now, find these sums and add them:
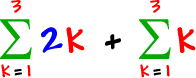
Do you believe it? (You should have gotten the same thing for both.)
This may not seem like a big deal, but you'll need it to prove some important calculus stuff, so let's get used to it.
Here's the proof:
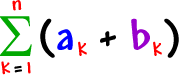 |
Just expand it out... |
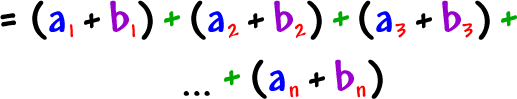
Now, use the commutative and associative properties... Gather up the a's... Gather up the b's...

Here are the other two properties -- I'll let you do the proofs:
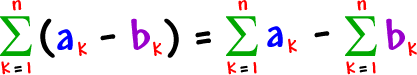 |
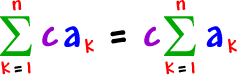 |