123
of 3

Sequences with Formulas

Remember when I did that list with the a's to describe a sequence...

a1 , a2 , a3 , a4 , ... , an , ...
And I told you this was the nth term?

That probably didn't mean much to you at the time.  Here's what we use this for:

The nth term is given by a formula.
We can use this formula to build the sequence.

Check it out:

Let's build the sequence whose nth term is given by

an = 2^n - 3n

See the n's in this guy arrow ?

If we let n = 1, we'll get the first term of the sequence:

n = 1 ... a1 = 2^1 - 3 ( 1 ) = -1

If we let n = 2, we'll get the second term:

a2 = 2^2 - 3 ( 2 ) = -2

If we let n = 3, we'll get the third term:

a3 = 2^3 - 3 ( 3 ) = -1

and so on...

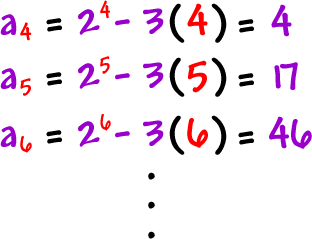
a4 = 2^4 - 3 ( 4 ) = 4 ... a5 = 2^5 - 3 ( 5 ) = 17 ... a6 = 2^6 - 3 ( 6 ) = 46 ...

So, our sequence is

-1 , -2 , -1 , 4 , 17 , 46 , ...

It's easy!

When you're given a formula for  an , you stick in n = 1, then
n = 2, then 3, 4, and 5 to get the first five terms.

TRY IT:

Build the sequence (the first five terms) whose nth term is given by

an = 6n - 4