A GEOMETRIC EXAMPLE:

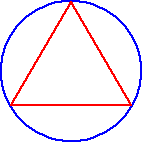
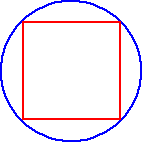
Let's look at a polygon inscribed in a circle... If we increase the number of sidesof the polygon, what can you say about the polygon with respect to the circle?

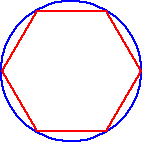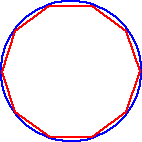As the number of sides of the polygon increase, the polygon is getting closer and closer to becoming the circle!

If we refer to the polygon as an n-gon, where n is the number of sides, we can make some equivalent mathematical statements. (Each statement will get a bit more technical.)

• As n gets larger, the n-gon gets closer to being the circle.
• As n approaches infinity, the n-gon approaches the circle.
• The limit of the n-gon, as n goes to infinity, is the circle!

The n-gon never really gets to be the circle, but it will get darn close! So close, in fact, that, for all practical purposes, it may as well be the circle. That's what limits are all about!

Archimedes used this idea (WAY before Calculus was even invented) to find the area of a circle before they had a value for PI! (They knew PI was the circumference divided by the diameter... But, hey, they didn't have calculators back then.)