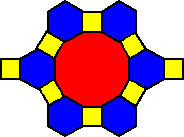
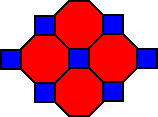
To name a tessellation, simply work your way around one vertex counting the number of sides of the polygons that form that vertex. The trick is to go around the vertex in order so that the smallest numbers possible appear first.

That's why we wouldn't call our 3, 3, 3, 3, 6 tessellation a 3, 3, 6, 3, 3!

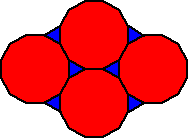
Here's another tessellation made up of hexagons and triangles.

Can you see why this isn't an official semi-regular tessellation?

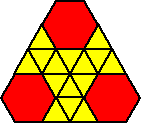
It breaks the vertex rule! Do you see where?

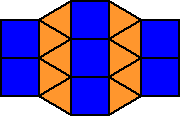
Here are some tessellations using squares and triangles:

Can you see why this one won't be a semi-regular tessellation?

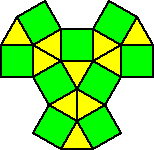
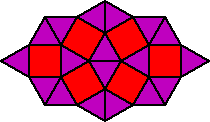
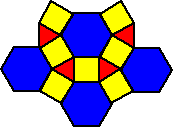
MORE SEMI-REGULAR TESSELLATIONS

What others semi-regular tessellations can you think of?