So far, we've learned how to add and subtract matrices (the sizes had to be the same) and how to multiply a matrix by a scalar.  These were really easy.

Multiplying two matrices is a bit tricky, but, once you get the hang of it, it's a snap -- you just need to be careful!

First of all, the size of the two matrices you are multiplying is super important!

Here's how it works:

Say the size of matrix A is 3 x 4
and the size of matrix B is 4 x 1
and we want  ...

Looking at the sizes...

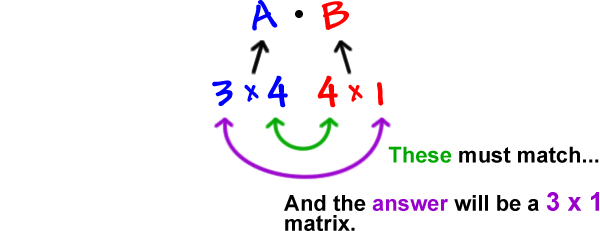
You'll see this when we do one.

In general:

If the size of matrix A is m x n
and the size of matrix B is n x p,

then

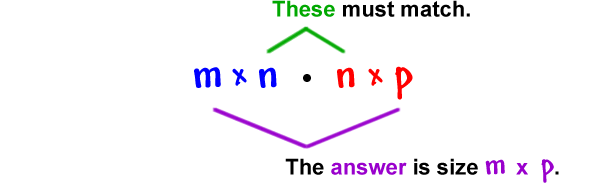
This is for  ...

Can we multiply ?  No!

 

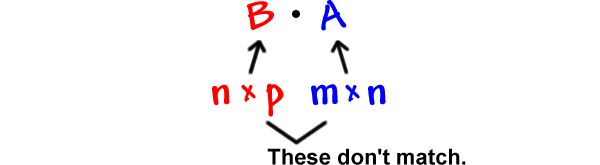
For this to all make sense, we really just need to do one.