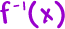123
of 3

How to Find the Inverse of a Function

Remember, you've got two ways you can double-check this answer to see if it's right:

 Graphf( x )andf^( -1 )( x )on the same graph and
  see if they're mirror images over the line y = x.
(Easy -- since these are both lines.)

Do it!

 Find either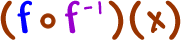( f o f^-1 )( x ) or( f^-1 o f )( x )
 (or both for practice!)

*Note:  This is just like ( f o g )( x ), but with different notation.

OK, here's the list of steps:

How to find the inverse of a function:

          STEP 1:  Stick a "y" in for the "f(x)."

          STEP 2:  Switch the x and y.

          STEP 3:  Solve for y.

 STEP 4:  Stick    f^( -1 )( x )in for the "y."

THEN, CHECK IT!