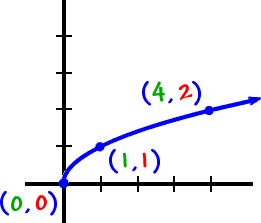
Let's look at another example:
With the two previous things in mind, can you draw the inverse of this?
![]()
| Since we don't know what the graph of | looks | |
| like yet (well, I do... but you don't), let's plot a few points: | ||
 |
It's just a half a parabola |
Cool! So, what are the two things?
| They are symmetric with respect to y = x |
| Every (x, y) has a (y, x) partner |
Now, you can graph the inverse!
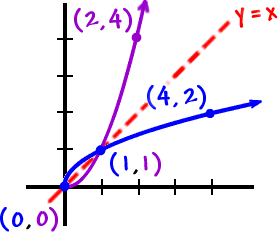 |
Hey! It's half of Standard Parabola Guy!
|
| Now, I can tell you why I said | for these guys in the last | |
| lesson! | ||
| and |