Rule

These guys in the set are just like ( x , y ) points on a graph...

So, we can actually graph this thing:

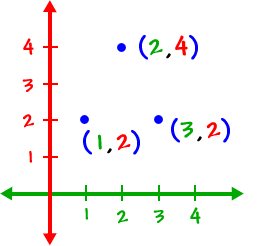* Don't connect the dots!   These are isolated points and   this isn't a coloring book!

Just like before, the x guys are our input guys -- the domain:

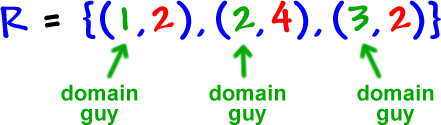
And remember that y guys are really f(x) guys -- range guys:

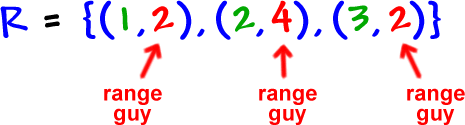
OK, so how can I tell if this guy is a function or not?  There are two ways:  The vertical line test (which we'll stick with) and another way that uses cool domain and range blobs (which you'll probably see if you go on to take some harder courses in math.)

Here's the vertical line test way -- but, now I want to be sophisticated and use the official definition:

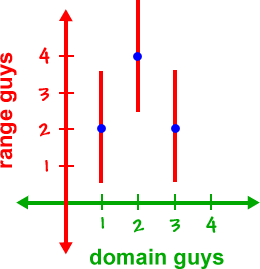Yes, R is a function since each element in the domain goes to exactly one element in the range. (It passes the vertical line test.)