Solving 3 x 3 systems of equations works a lot like the 2 x 2 method of elimination -- with a little substitution mixed in.  It really isn't hard, but it takes good organization skills.  The problems are a bit long, but I'll show you how to work through them and how to keep things organized.

Instead of starting out by working through an entire problem (which would look pretty creepy), let's start with some that are almost finished already.

Remember that our goal is to find the values for x, y and z.  (or whatever letters you have.)

Let's finish solving this guy...  As you can see, we already know what zis!

What we're going to do is called "back substitution" because we're going to work our way back up through the equations, starting at the bottom with 
that z.

Take the value for z and stick it into the equation with two variables... This will pop the y!
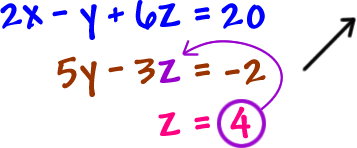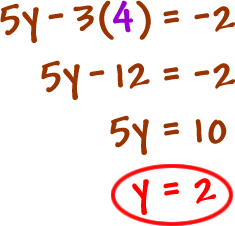