12
of 2

Solving by Graphing

Systems, 2 x 2 in this case, are when you have 2 equations and 2 unknowns (letters).

Here's an example:

x + y = 3

x - 2y = 0

The goal is to find an x guy and a y guy that work in both equations.

In this chapter, I'll show you three different ways to solve these.

The first method is graphing.  This is a cool method to start with since it lets you see what's going on.

We've got two equations -- and they are equations of lines.  Let's graph them both on the same axes and see what we get.

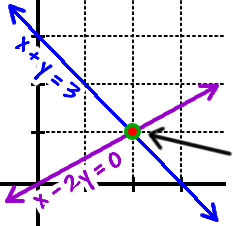the graph of x + y = 3 and x - 2y = 0 ... they cross at ( 2 , 1 ) Hey, the two lines intersect at the point ( 2 , 1 ) .

This means that ( 2 , 1 ) is a point in BOTH lines...

So, x = 2 and y = 1 will work in the equations!

x + y = 3 ... 2 + 1 = 3 ... yep

x - 2y = 0 ... 2 - 2 ( 1 ) = 0 ... yep

 

So, the answer is  ( 2 , 1 )  .

Checking your answers, like we did at the end there, is a really good idea... and something you should always do on a test!  We're going to do it on every single problem we do!