12
of 2

A Brief Intro

Actually, we've already been working with quadratics. They are the trinomial guys we've been factoring:

x^2 - x - 6

2y^2 - 8y - 10

What makes them quadratics is that they are 2nd degree polynomials.

(They have a squared guy like     x^2
 		     or   y^2   .)

Now, we're going to be solving equations with them like

x^2 - x - 6 = 0

2y^2 - 8y - 10 = 0

Here's the big official form of a quadratic equation:

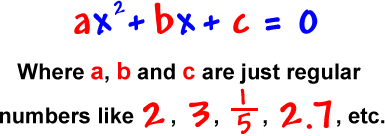ax^2 + bx + c = 0 where a, b and c are just regular numbers like 2, 3, 1/5, 2.7, etc.

Examples:

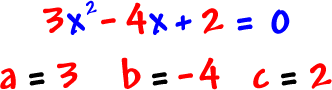
3x^2 - 4x + 2 = 0 ... a = 3, b = -4, c = 2

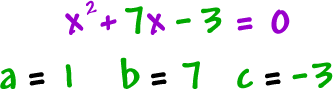
x^2 + 7x - 3 = 0 ... a = 1, b = 7, c = -3

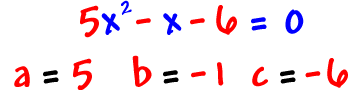
5x^2 - x - 6 = 0 ... a = 5, b= -1, c = -6

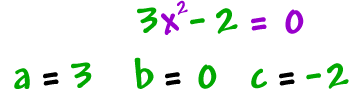
3x^2 - 2 = 0 ... a = 3, b = 0, c = -2

 

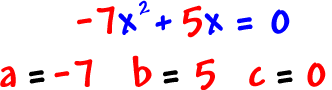
-7x^2 + 5x = 0 ... a = -7, b = 5, c = 0

It would be silly to ever have a = 0 in a quadratic -- Then we wouldn't have a squared guy!