The Properties of a Rectangle

Definitions and formulas for the perimeter of a rectangle, the area of a rectangle, how to find the length of the diagonal of a rectangle, properties of the diagonals of a rectangle

Just scroll down or click on what you want and I'll scroll down for you!

perimeter of a rectangle	area of a rectangle	properties of the sides and angles of a rectangle
diagonal of a rectangle	properties of the diagonals of a rectangle

The perimeter of a rectangle:
	To find the perimeter of a rectangle, just add up all the lengths of the sides: Perimeter = L + w + L + w = 2L + 2w

The area of a rectangle:
	To find the area of a rectangle, just multiply the length times the width: Area = L x w

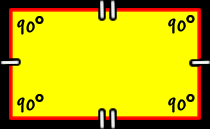
The sides and angles of a rectangle:

rectangle

Opposite sides of a rectangle are the same length (congruent).

The angles of a rectangle are all congruent (the same size and measure.)

Remember that a 90 degree angle is called a "right angle." So, a rectangle has four right angles.

Opposite angles of a rectangle are congruent.

Opposite sides of a rectangle are parallel.

Properties of the diagonals of a rectangle:
	As you can see from the pictures to the left, the diagonals of a rectangle do not intersect in a right angle (they are not perpendicular). (Unless the rectangle is a square.) And the angles formed by the intersection are not always the same measure (size). Opposite central angles are the same size (they are congruent.)

	The pieces created when the diagonals intersect are congruent.

The Properties of a Rectangle

welcome to coolmath