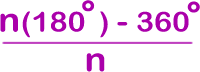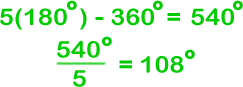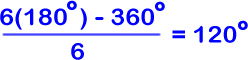METHOD 2:
This method will be very similar to that of the first method. Except that we will draw our triangles using a point drawn inside the polygon.
|
|
| ||
4 sides, 4 triangles | 5 sides, 5 triangles | 6 sides, 6 triangles |
Notice that not all of the angles of the triangles are involved with the interior angles of the polygons. We'll need to figure out how to deal with that.
Starting with the square:
4 triangles... ![]()
At this point in method 1, we had 360... So we are off by 360. But we haven't dealt with the fact that those middle angles are not involved with the interior angles of the square. It turns out that the sum of the angles around that middle point is 360!
So ![]()
and 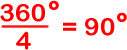
Let's try the pentagon...
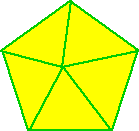 | 5 triangles...
|
Can you figure out the hexagon?
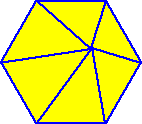 |
|
In general, the measure of an interior angle of a regular n-gon is