12345
of 5

Mathematic Induction

Prove
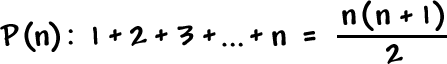
              P( n ): 1 + 2 + 3 + ... + n = n( n + 1 ) / 2

 

Here's another one:

Prove

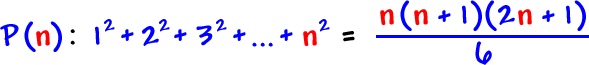
P( n ): 1^2 + 2^2 + 3^2 + ... + n^2 = n( n + 1 )( 2n + 1 ) / 6
 

1 )

 Show P( 1 ) is true:

Stick a 1 in for all the n's and show it works.
 

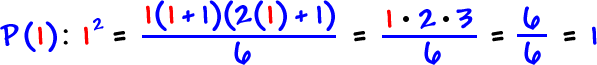
P( 1 ): 1^2 = 1( 1 + 1 )( 2( 1 ) + 1 ) / 6 = 1 * 2 * 3 / 6 = 6 / 6 = 1
 

So, P( 1 ) is true.

 

2 )

 Assume P( k ) is true:

Stick a k in for all the n's and say it's true.

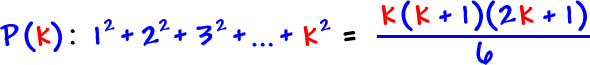
P( k ): 1^2 + 2^2 + 3^2 + ... + k^2 = k( k + 1 )( 2k + 1 ) / 6

is true
 

 

3 )

 Show P( k ) --> P( k + 1 )

Use P( k ) to show that P( k + 1 ) is true.

Write out your goal by sticking ( k + 1 ) in for all the n's... Leave the k on the left side.

GOAL: P( k + 1 ): 1^2 + 2^2 + 3^2 + ... + k^2 + ( k + 1 )^2 = ( k + 1 )[ ( k + 1 ) + 1 ][ 2( k + 1 ) + 1 ] / 6

Start with the left side of the P( k + 1 ) and slowly turn it into the right side... Don't confuse the monkey!
 

P( k + 1 ): 1^2 + 2^2 + 3^2 + ...+ k^2 + ( k + 1)^2 ... Use P( k )! = k( k +1 )( 2k + 1 ) / 6 + ( k + 1 )^2 ... need that 6 and one big fraction ... k( k + 1 )( 2k +1 ) / 6 + 6( k + 1 )^2 / 6 = k( k + 1 )( 2k + 1 ) + 6( k + 1 )^2 / 6


Look at the end goal... What's in front? ... Factor it out!
 

= ( k + 1 )[ k( 2k + 1 ) + 6( k + 1 ) ] / 6 ... Simplify this end part... = ( k + 1 )[ 2k^2 + k + 6k + 6 ] / 6 ... ( k + 1 )( 2k^2 + 7k + 6 ) / 6 ... factor this... it MUST work! ... You can look at the goal to cheat! ... = ( k + 1 )( k + 2 )( 2k + 3 ) / 6 ... now, make these last parts look like the goal ... = ( k + 1 )[ ( k +1 ) + 1 ][ 2k + 2 + 1 ] / 6 = ( k + 1 )[ ( k + 1 ) + 1 ][ 2( k + 1 ) + 1 ] / 6

 

So, P( k ) --> P( k + 1 )

 

4 )

 Thus, P( n ) is true.  []

 

OK, you need the practice...  Write this guy out without my [ boxed ]
comments.