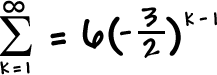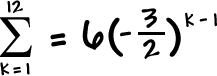123456
of 6

Geometric Series

YOUR TURN:

Find the sum

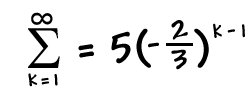
the summation of ( 5( -2 / 3 )^( k - 1 ) ) as k goes from 1 to infinity

But, we're not quite done yet.

Our formula only works when | r | < 1 .
So, what if r is something like 5 / 2 ?  Then the series does not have
a sum.  It shoots off to infinity.  When this happens, we call the series "divergent."

So, if someone asks you to find the sum of an INFINITE geometric sequence, CHECK THE RATIO!

If | r | < 1 , crunch the sum.
If | r | is not less than 1 , say something like

"There's no finite sum.  This critter's divergent!"

 

TRY IT:

Find the sums (if possible):

the summation of ( 6( -3 / 2 )^( k - 1 ) ) as k goes from 1 to infinity
 

the summation of ( 6( -3 / 2 )^( k - 1 ) ) as k goes from 1 to 12