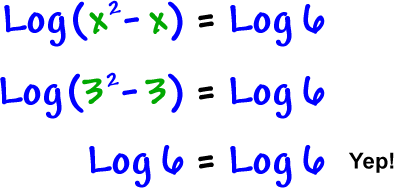Hey, you know... We'd better start checking our answers to make sure they're OK!
| Check x = 3: |
|
| Check x = -2: |
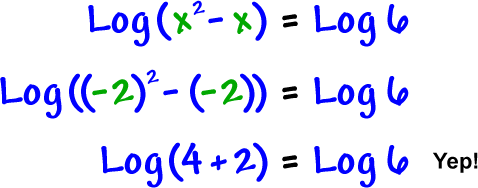 |
So, in this case, our answers are both good.
One thing you always need to watch out for is an answer that breaks a log's biggest rule:
| You can't take the log of a negative number! |
Why not?
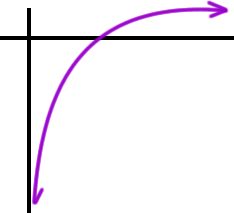
Look again at the log's graph:
| Logarithms only exist in positive x values! So, Log 0 doesn't exist! Log (-5) doesn't exist! |
 |
Teachers love sneaking these guys in for answers... So, keep an eye out!
Watch out for x's that give Log 0, too!
YOUR TURN:
| Solve |