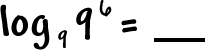THEY UNDO EACH OTHER!
So...
|
|
and |
|
undo each other! |
|
|
and |
|
undo each other! |
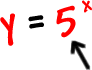 |
and |
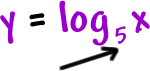 |
undo each other! |
| Notice that the bases match on all of these. | |||
So, in general,
|
|
and |
|
undo each other! |
Why am I putting
exclamation points on all of these? Because this is VERY
exciting stuff (and I'm a geek). Just wait until the next
section
-- we'll be able to solve equations with this stuff!
Here's how you usually see these tricks written:
|
|
| Here are some examples of rule |
|
: |
|
|
|
|
TRY IT:
|
|
|
| Here are some examples of rule |
|
: |
|
|
|
|
TRY IT:
|
|
|