Most simply put, logarithms are inverses of exponentials.

Check it out:

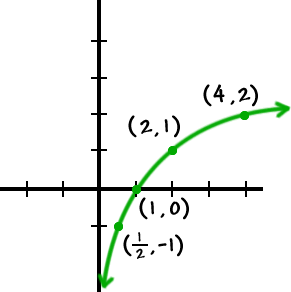
Let's graph the inverse of

Remember that every ( x , y ) has a ( y , x ) partner, so we'll graph this guy...  then nail his inverse!

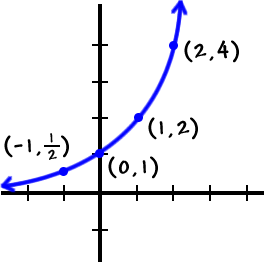This is the inverse of

Remember the steps to find the inverse of a function using algebra?  In one part, you switch the x and the y -- right?

So, we COULD say that the inverse of

is

...

But...  ya know...  in math, we really like to write things like