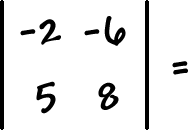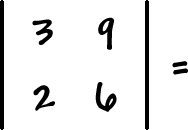A determinant (which uses vertical lines instead of brackets)
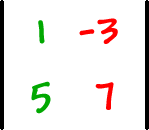
will give us a number that goes along with the matrix. We'll be able to use these numbers to solve systems! Woo hoo!
OK, so here's how you get the determinant -- it's really easy:
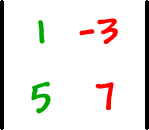 |
|
Here's what I did:
I multiplied down this diagonal...
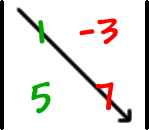 |
|
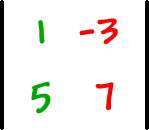 |
|
Put a minus... |
then multiplied up this diagonal...
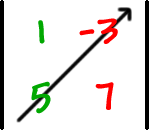 |
|
Here's the general formula:
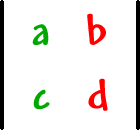 |
|
TRY IT: