123
of 3

Graphing by Completing the Square - Freaky Things That Can Happen

Completing the square is pretty easy when the coefficient on the x^2  is one...

When it isn't, things get a little sticky.

Let's do this guy:

y = 3x^2 + 12x + 11

STEP 1: Like before...

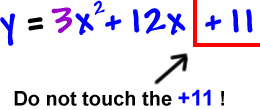
y = 3x^2 + 12x + 11 ... do not touch the +11 !

STEP 2: Identify the trouble-maker:

Who's a problem?

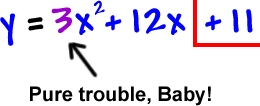
y = 3x^2 + 12x + 11 ... the 3 is pure trouble, baby!

We CANNOT complete the square with this 3 here -- the x^2 must be alone!  So, we factor him out...  of both x guys -- not the 11!  You can't touch him.

y = 3 ( x^2 + 4x ) + 11

Now, we an go ahead with the rest of the process.  Just don't forget about that 3 who's hanging around in the front.

STEP 3:

y = 3 ( x^2 + 4x ___ ) + 11 ___

STEP 4:

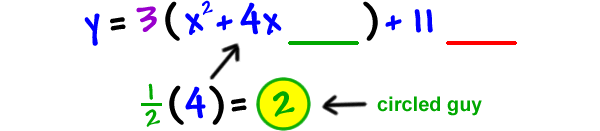
y = 3 ( x^2 + 4x ___ ) + 11 ___ ... 1/2 ( 4 ) = 2 ( circled guy )

STEP 5:

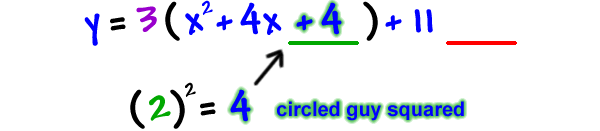
y = 3 ( x^2 + 4x + 4 ) + 11 ___ ... ( 2 )^2 = 4 ( circled guy squared )

STEP 6: Remember to balance it out! 
                  But, be careful...  IT'S A TRAP!

How much weight did we really add on?

4 pounds?  NO!

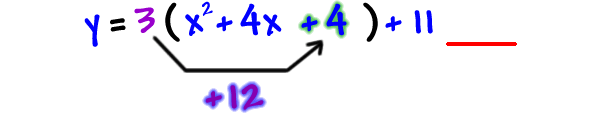
y = 3 ( x^2 + 4x + 4 ) + 11 ___ ... the 3 distributes to the +4 to give +12

We really plunked on 12 pounds because the 3 distributes to the 4!

So, take 12 pounds off on the end:

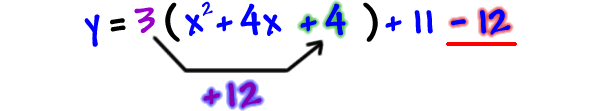
y = 3 ( x^2 + 4x + 4 ) + 11 - 12 ... the 3 distributes to the +4 to give +12 ... undo it with the -12

STEP 7: Finish it off...  Where's circled guy?

y = 3 ( x + 2 )^2 - 1 ... 2 is circled guy

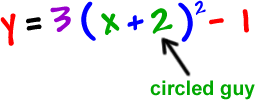
Done! He's ready to graph!

I'll let you do that!