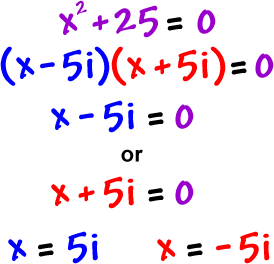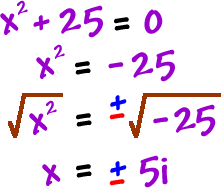12
of 2

Complex Numbers in the Quadratic Formula

Now, try solving this guy:

x^2 + 25 = 0

  WAY 1: FACTOR   WAY 2: SQUARE ROOT TRICK

x^2 + 25 = 0 gives ( x - 5i ) ( x + 5i ) = 0 which gives x - 5i = 0 or x + 5i = 0 which gives x = 5i or x = -5i

{ -5i , 5i }

 

x^2 + 25 = 0 gives x^2 = -25 which gives sqrt( x^2 ) = +/- sqrt( -25 ) which gives x = +/- 5i

 

{ -5i , 5i }

Your turn...  and do it both ways:

Solve  x^2 + 81 = 0

Hey, have you noticed something interesting with all our answers?

{ 3 - 4i , 3 + 4i }

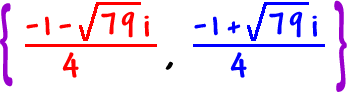
{ ( -1 - sqrt( 79 ) i ) / 4 , ( -1 + sqrt( 79 ) i ) / 4 }

{ -5i , 5i }
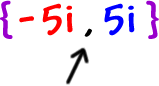
Look at this last guy in his official complex form:

{ 0 - 5i , 0 + 5i }

Each of these answers is a pair -- one with a minusand one with a plus.  Like

{ a - bi , a + bi }

These are called complex conjugates.  For example, the conjugate of

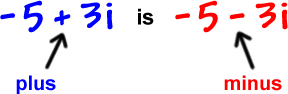
-5 + 3i is -5 - 3i ... the first one is plus is the second is minus

When you are solving quadratic equations, each complex solution will ALWAYS have his conjugate buddy with him!